[Python] 이것이 코딩테스트다 8장 다이나믹 프로그래밍
다이나믹 프로그래밍의 핵심
🔑 수열의 점화식을 구하는 것이 핵심!
중복되는 연산을 줄이자. 연산 속도와 메모리공간을 최대한으로 활용할 수 있는 효율적인 알고리즘을 작성
현재의 항들로 다음 항을 구할 수 있는 경우 다이나믹 프로그래밍을 쓴다.
대표적 예시 >> 피보나치 수열
- 재귀 함수(탑다운 방식)
구현하긴 간편하지만 숫자가 커지면 기하급수적으로 연산횟수가 늘어난다.
f(100)을 구하기 위해서는 약 1,000,000,000,000,000,000,000,000,000,000번 연산을 해야한다. 시간으로 따지면 수백억년이 넘어가는 시간이 걸림.
- 다이나믹 프로그래밍 (보텀업 방식)
하지만 다이나믹으로 풀 경우, 같은 문제라면 한번 씩만 풀어 저장해 놓기 때문에 효율적으로 해결하게 된다. O(N)의 성질을 보임.
다이나믹 프로그래밍을 이용하여 피보나치 수열 문제를 풀었던 방법을 잘 알아두면 다른 다이나믹 프로그래밍 문제에 접근 하는 방법 또한 떠올릴 수 있다.
수열은 배열이나 리스트, 딕셔너리로 표현하여 이용할 수 있다.
코딩 테스트
코딩 테스트에서 다이나믹 프로그래밍은 비교적 간단한 형태. 물론 3차원 리스트를 이용하여야 하는 복잡한 난이도의 문제가 출제될 수도 있다.(최단경로, 플로이드)
- 메모이제이션: 엄밀히 말하면 이전에 계산된 결과를 일시적으로 기록해 놓은 넓은 개념 . 탑다운에 사용되는 표현
- 다이나믹 프로그래밍: 보텀업방식을 사용하여 사용되는 결과를 DP테이블에 기록해 놓은것.
----------------------------------시간제한 참고
파이썬 => 1초 20000000번 연산
데이터 20,000,000 => O(N)
데이터 1,000,000 => O(NlogN)
데이터 4~5,000 => O(N^2)
다이나믹 프로그래밍 예제
📝 체감난이도 : ★☆☆☆☆
🎨 피보나치 수열 : 재귀
🎨 피보나치 수열 : 다이나믹 이용한 재귀
🎨 피보나치 수열 : 다이나믹 이용한 반복문
🔑 Key Point
다이나믹을 이용할 때에는 배열에 바텀에서부터 계산한 결과를 저장해두어, 이미 계산된 결과라면 함수를 탈출하게 하는 if문을 하나 더 두었다.
1로 만들기
시간제한 1초 . 데이터 30,000개
📝 체감 난이도 : ★★★☆☆
🎨 내가 짠 코드 (이진 탐색)
🔑 Key Point
- 그리디 문제로 풀 수 없는 이유
이 문제를 처음 보면 그리디 방법을 생각 할 것.
하지만 그리디가 만족하려면 각각의 수가 배수관계에 있어야하는데 주어진 수는 5,3,2로,
그리디를 이용한다면 모든 경우에 대하여 최적의 해를 보장할 수 없다.
따라서, 다이나믹 프로그래밍 접근법을 의심해 보아야 한다.\
- 핵심 점화식
A(i) = min ( A(i-1)+1, A(i/2)+1, A(i/3)+1, A(i/5)+1)
A(i) = min ( A(i-1), A(i/2), A(i/3), A(i/5))+1
+1 을 해주는 이유는 이전 항을 정보를 가져올때 한번 연산이 수행되기 때문이다. 그리고 1은 공통적으로 더해주는 덧셈이기 때문에 min함수에서 뺄 수 있다.
위의 점화식을 이용하여 2부터 (바텀에서부터) 반복하여 DP테이블을 목적지 까지 채우면 된다.
개미 전사
시간제한 1초 . 데이터 100개
체감 난이도 : ★★★☆☆
🎨 내가 짠 코드
🔑 Key Point
점화식으로 푼다고 생각이 들었으면
왼쪽부터 차례대로 식량창고를 턴다고 생각하면 어렵지 않게 점화식을 세울수 있다
A[i] = max(A[i-1], A[i-2] + k(i))
처음 두가지 경우는 우선 dp테이블에 채워둔 뒤 2일때부터(바텀부터) 위의 점화식을 적용하여 목적지까지 채우면 쉽게 구할 수 있다.
코드는 매우 쉬운데, 점화식을 생각해 내는 것이 어려운 편이다.
바닥 공사
시간제한 1초 . 데이터 1000개
체감 난이도 : ★★★☆☆
🎨 내가 짠 코드
🔑 Key Point
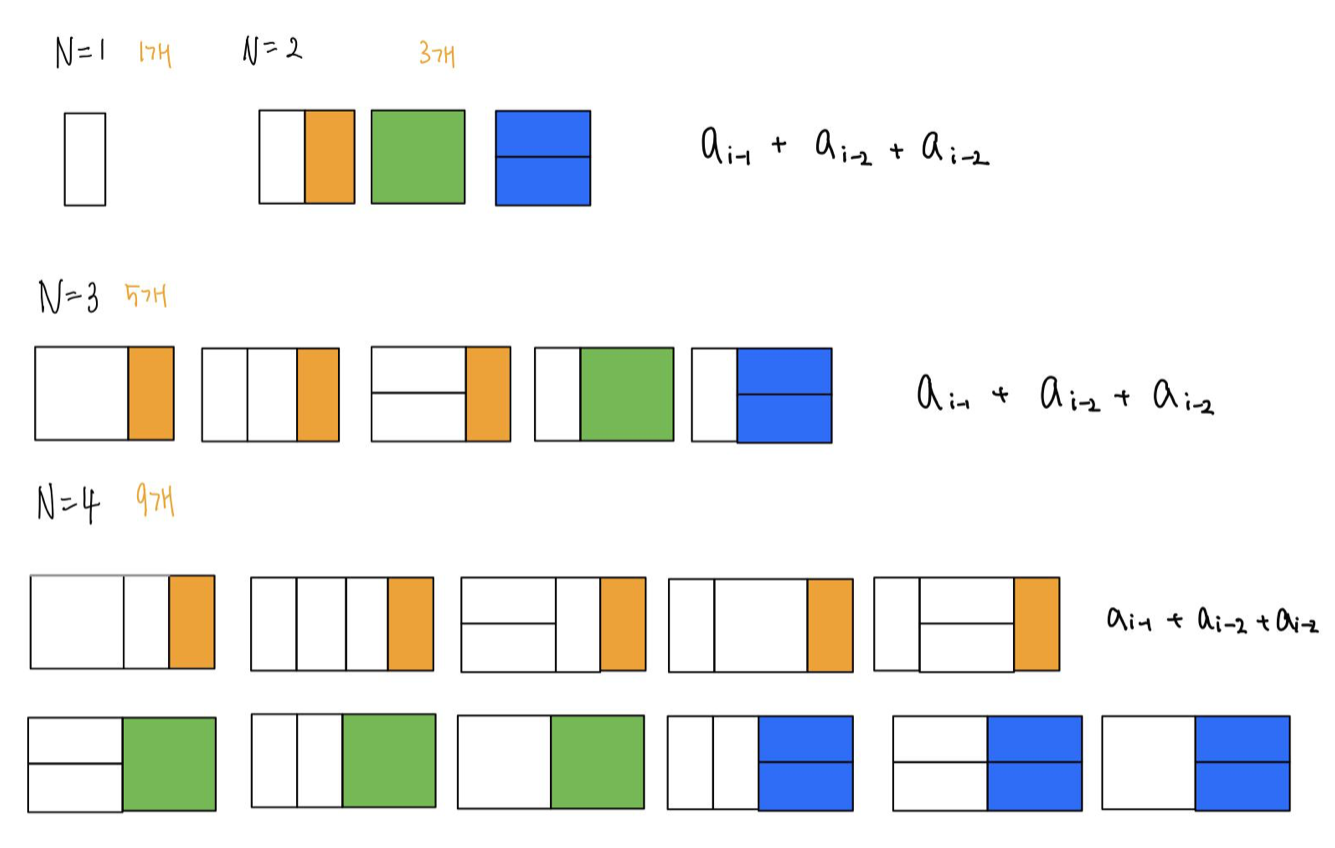
A[i] = A[i-1] + A[i-2] * 2
역시나 점화식 생각하기가 어려운 문제
타일 문제는 다이나믹 프로그래밍 중 대표적 기본문제라고 하니, 생각이 나지 않는다면 그림을 그려보아야 한다
A[0] = 0
A[1] = 1
A[2] = 3
으로 초기 설정 한 뒤, 3부터 위의 점화식을 반복하여, 구하고자 하는 목적지까지 채워주면 된다.
효율적인 화폐 구성
시간제한 1초. N = 100개, M =1000개
체감 난이도 : ★★★☆☆
🎨 내가 짠 코드
🔑 Key Point
주어진 화폐를 가지고 목적 화폐를 구성할 수도 있고 구성하지 못할 수도 있다. 화폐가 배수 관계가 아닐 수 있기 때문에 그리디 보단 다이나믹을 떠올려야하며,
바텀업으로 dp테이블을 채워나간다.
배열을 초기에 10,001로 초기해 놓는다( 10,000까지 나올수 있다 했으므로)
핵심 점화식
A[i] = min(A[i], A[i - coins[j]] +1)
마무리
다이나믹은 점화식이 넘 어렵다.
자꾸 수학때 생각이 나서 계산을 하려하는데 , 계산은 컴퓨터가 해주므로 우리는 점화식만 세우면 된다
연습이 필요한 부분 같다